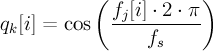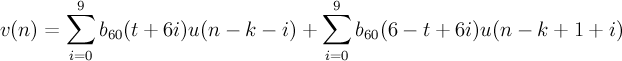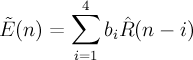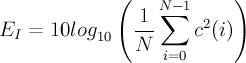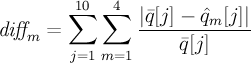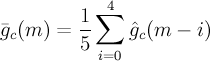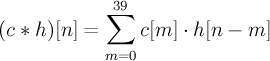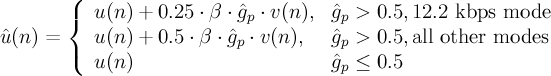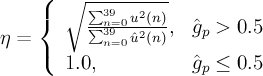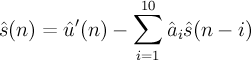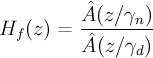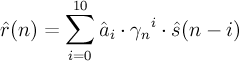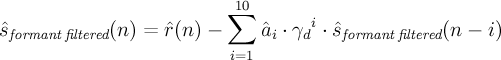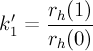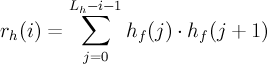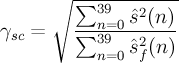AMR-NB-WIP: Difference between revisions
| (7 intermediate revisions by the same user not shown) | |||
| Line 849: | Line 849: | ||
; ^a_i : LP filter coefficients | ; ^a_i : LP filter coefficients | ||
Note: for n | Note: for n-i < 0, ^s(n-i) should be take from previous speech samples if existing, else we will consider them 0 as this behaviour is undefined the specification. | ||
== Additional instability protection == | == Additional instability protection == | ||
| Line 871: | Line 871: | ||
; γ_n, γ_d : control the amount of formant post-filtering | ; γ_n, γ_d : control the amount of formant post-filtering | ||
The speech samples, ^s(n), are filtered through ^A(z/γ_n) to produce the residual signal ^r(n). | |||
[[Image: Amrnb_residual.gif]] | |||
^r(n) is filtered through 1/^A(z/γ_d). | |||
[[Image: Amrnb_fmntfilt.gif]] | |||
The output is filtered through H_t(z) (the tilt compensation filter) resulting in the post-filtered speech signal, ^s_f(n). | |||
[[Image: Amrnb_pftilt.gif]] | [[Image: Amrnb_pftilt.gif]] | ||
[[Image: Amrnb_mu.gif]] | |||
[[Image: Amrnb_reffac.gif]] | [[Image: Amrnb_reffac.gif]] | ||
| Line 880: | Line 890: | ||
[[Image: Amrnb_r_h.gif]] | [[Image: Amrnb_r_h.gif]] | ||
; L_h : 22 - the truncation of the impulse response | |||
; h_f : impulse response of the formant filter H_f | |||
So, in summation notation: | |||
[[Image: Amrnb_pftiltsum.gif]] | |||
===== 12.2 and 10.2 kbps modes ===== | ===== 12.2 and 10.2 kbps modes ===== | ||
| Line 913: | Line 928: | ||
(c.f. §6.2.2) | (c.f. §6.2.2) | ||
[[Image: Amrnb_highpass.gif]] | |||
After completing all filtering, the samples are scaled up by a factor of 2. | |||
Latest revision as of 12:56, 24 September 2007
This text aims to be a simpler and more explicit document of the AMR narrow band decoding processes to aid in development of a decoder. Reference to sections of the specification will be made in the following format: (c.f. §5.2.5). Happy reading.
Nomenclature weirdness
Throughout the specification, a number of references are made to the same (or very similar) items with fairly confusing variation. They are listed below to aid understanding of the following text but efforts will be made to consistently use one item name throughout or to use both with the lesser used name in parenthesis.
- Pitch / Adaptive codebook
- Fixed / Innovative (also algebraic when referring to the codebook)
- Quantified means not quantised
Summary
- Mode dependent bitstream parsing
- Indices parsed from bitstream
- Indices decoded to give LSF vectors, fractional pitch lags, innovative code vectors and the pitch and innovative gains
- LSF vectors converted to LP filter coefficients at each subframe
- Subframe decoding
- Excitation vector = adaptive code vector * adaptive (pitch) gain + innovative code vector * innovative gain
- Excitation vector filtered through an LP synthesis filter to reconstruct speech
- Speech signal filtered with adaptive postfilter
Bitstream parsing
Documented on http://wiki.multimedia.cx/index.php?title=AMR-NB and in 26.101
For implementation, see http://svn.mplayerhq.hu/soc/amr/amrnbdec.c?view=markup
Decoding of LP filter parameters
The received indices of LSP quantization are used to reconstruct the quantified LSP vectors. (c.f. §5.2.5)
12.2kbps mode summary
- indices into code books are parsed from the bit stream
- indices give elements of split matrix quantised (SMQ) residual LSF vectors from the relevant code books
- prediction from the previous frame is added to obtain the mean-removed LSF vectors
- the mean is added
- the LSF vectors are converted to cosine domain LSP vectors
Decoding SMQ residual LSF vectors
The elements of the SMQ vectors are stored at an index into a code book that varies according to the mode. There are 5 code books for the 12.2kbps mode corresponding to the 5 indices. These tables will be referred to as:
lsf_m_n
- m
- the number of indices parsed according to the mode
- n
- the index 'position' i.e. 1 for the first index, etc
The 5 indices are stored using 7, 8, 8 + sign bit, 8, 6 bits respectively. The four elements of a 'split quantized sub-matrix' are stored at the index position in the appropriate code book are:
- 1st index in 1st code book
- r1_1, r1_2, r2_1, r2_2
- 2nd index in 2nd code book
- r1_3, r1_4, r2_3, r2_4
- 3rd index in 3rd code book
- r1_5, r1_6, r2_5, r2_6
- 4th index in 4th code book
- r1_7, r1_8, r2_7, r2_8
- 5th index in 5th code book
- r1_9, r1_10, r2_9, r2_10
With rj_i :
- j
- the first or second residual lsf vector
- i
- the coefficient of a residual lsf vector ( i = 1, ..., 10 )
- rj_i
- residual line spectral frequencies (LSFs) in Hz
Mean-removed LSF vector prediction
- z_j(n)
- the mean-removed LSF vector at the jth subframe
- r_j(n)
- prediction residual vector of frame n at the jth subframe
- ^r_2(n-1)
- the quantified residual vector from the previous frame at the 2nd subframe
The mean is added
- lsf_mean_m
- a table of the means of the LSF coefficients
- m
- the number of indices parsed according to the mode
- fj
- the LSF vectors
LSF to LSP vector conversion
- q_k[i]
- the ith coefficient of the kth line spectral pair (LSP) in the cosine domain
- k
- the two lsf vectors give the LSP vectors q2, q4 at the 2nd and 4th subframes; k = 2*j
- f_j[i]
- ith coefficient of the jth LSF vector; [0,4000] Hz
- f_s
- sampling frequency in Hz (8kHz)
Other active modes summary
The process for the other modes is similar to that for the 12.2kbps mode.
- indices into code books are parsed from the bit stream
- indices give elements of a split matrix quantised (SMQ) residual LSF vector from the relevant code books
- prediction from the previous frame is added to obtain the mean-removed LSF vector
- the mean is added
- the LSF vector is converted to a cosine domain LSP vector
Decoding the SMQ residual LSF vector
The 3 indices are stored with the following numbers of bits:
| Mode (kbps) | 1st index (bits) | 2nd index (bits) | 3rd index (bits) |
|---|---|---|---|
| 10.2 | 8 | 9 | 9 |
| 7.95 | 9 | 9 | 9 |
| 7.40 | 8 | 9 | 9 |
| 6.70 | 8 | 9 | 9 |
| 5.90 | 8 | 9 | 9 |
| 5.15 | 8 | 8 | 7 |
| 4.75 | 8 | 8 | 7 |
The four elements of a 'split quantized sub-matrix' are stored at the index position in the appropriate code book are:
- 1st index in 1st code book
- r_1, r_2, r_3
- 2nd index in 2nd code book
- r_4, r_5, r_6
- 3rd index in 3rd code book
- r_7, r_8, r_9, r_10
- r_i
- residual LSF vector (Hz)
- i
- the coefficient of vector ( i = 1, ..., 10 )
Mean-removed LSF vector prediction
- z_j(n)[i]
- the ith coefficient of the mean-removed LSF vector at the jth subframe
- r_j(n)[i]
- the ith coefficient of the prediction residual vector of frame n at the jth subframe
- pred_fac[i]
- the ith coefficient of the prediction factor
- ^r_j(n-1)[i]
- the ith coefficient of the the quantified residual vector of the previous frame at the jth subframe
These processes give the LSP vector at the 4th subframe (q4)
LSP vector interpolation (c.f. §5.2.6)
12.2 kbps mode
Other modes
LSP vector to LP filter coefficient conversion (c.f. §5.2.4)
for i=1..5
f1[i] = 2*f1[i-2] - 2*q[2i-1]*f1[i-1]
for j=i-1..1
f1[j] += f1[j-2] - 2*q[2i-1]*f1[j-1]
end
end
f1[-1] = 0; f1[0] = 0;
Same for f2[i] with q[2i] instead of q[2i-1]
for i=1..5 f'1[i] = f1[i] + f1[i-1] f'2[i] = f2[i] - f2[i-1] end
for i=1..5 a_i = 0.5*f'1[i] + 0.5*f'2[i] end for i=6..10 a_i = 0.5*f'1[11-i] - 0.5*f'2[11-i] end
- a_i
- the LP filter coefficients
Decoding of the pitch (adaptive codebook) vector
- indices parsed from bitstream
- indices give integer and fractional parts of the pitch lag
- pitch vector v(n) is found by interpolating the past excitation u(n) at the pitch lag using an FIR filter. (c.f. §5.6)
Decode pitch lag
Note: division in this section is integer division!
12.2kbps mode - 1/6 resolution pitch lag
First and third subframes
In the first and third subframes, a fractional pitch lag is used with resolutions:
- 1/6 in the range [17 3/6, 94 3/6]
- 1 in the range [95, 143]
...encoded using 9 bits.
For [17 3/6, 94 3/6] the pitch index is encoded as:
pitch_index = (pitch_lag_int - 17)*6 + pitch_lag_frac - 3;
- pitch_lag_int
- integer part of the pitch lag in the range [17, 94]
- pitch_lag_frac
- fractional part of the pitch lag in 1/6 units in the range [-2, 3]
so...
if(pitch_index < (94 4/6 - 17 3/6)*6) // fractional part is encoded in range [17 3/6, 94 3/6] pitch_lag_int = (pitch_index + 5)/6 + 17; pitch_lag_frac = pitch_index - pitch_lag_int*6 + (17 3/6)*6;
And for [95, 143] the pitch index is encoded as:
pitch_index = (pitch_lag_int - 95) + (94 4/6 - 17 3/6)*6;
- pitch_lag_int
- integer pitch lag in the range [95, 143]
so...
else // only integer part encoded in range [95, 143], no fractional part pitch_lag_int = pitch_index - (94 4/6 - 17 3/6)*6 + 95; pitch_lag_frac = 0;
Second and fourth subframes
In the second and fourth subframes, a pitch lag resolution of 1/6 is always used in the range [T1 - 5 3/6, T1 + 4 3/6], where T1 is nearest integer to the fractional pitch lag of the previous (1st or 3rd) subframe. The search range is bounded by [18, 143]. In this case the pitch delay is encoded using 6 bits and is therefore in the range [0,63].
So the search range for the pitch lag is:
search_range_min = max(pitch_lag_int_prev - 5, 18);
search_range_max = search_range_min + 9;
if(search_range_max > 143) {
search_range_max = 143;
search_range_min = search_range_max - 9;
}
- pitch_lag_int_prev
- the integer part of the pitch lag from the previous sub frame
The pitch index is encoded as:
pitch_index = (pitch_lag_int - (search_range_min - 1))*6 + pitch_lag_frac - 3;
- pitch_lag_int
- the integer part of the pitch lag in the range [search_range_min - 1, search_range_max]
- pitch_lag_frac
- the fractional part of the pitch lag in the range [-2, 3]
The formula for the pitch_index has been chosen to map pitch_lag_int [search_range_min - 1, search_range_max] and pitch_lag_frac [-2, 3] to [0,60]. (pitch_index = [0, 10]*6 + [-2, 3] - 3 = [0, 6, ..., 60] + [-5, 0] = [0,60])
So the pitch lag is calculated through:
// integer part of pitch lag = position in range [search_range_min - 1, search_range_max] + lower bound of range pitch_lag_int = (pitch_index + 5)/6 + search_range_min - 1; // fractional part of pitch lag = pitch index - (integer part without offset)*6 - 1 3/6 offset to bring the values to the correct range pitch_lag_frac = pitch_index - ((pitch_index + 5)/6)*6 - 9;
Note that when using integers and integer division to conduct (pitch_index + 5)/6 the result is similar to taking the ceiling of pitch_index/6.0.
Others modes - 1/3 resolution pitch lag
First and third subframes
In the first and third subframes, a fractional pitch lag is used with resolutions:
- 1/3 in the range [19 1/3, 84 2/3]
- 1 in the range [85, 143]
...encoded using 8 bits.
For [19 1/3, 84 2/3] the pitch lag is encoded as:
pitch_index = pitch_lag_int*3 + pitch_lag_frac - (19 1/3)*3;
- pitch_lag_int
- integer part of the pitch lag in the range [19, 84]
- pitch_lag_frac
- fractional part of the pitch lag in 1/3 units in the range [0, 2]
so...
if(pitch_index < (85 - 19 1/3)*3) // fractional part is encoded in range [19 1/3, 84 2/3] pitch_lag_int = (pitch_index + 2)/3 + 19; pitch_lag_frac = pitch_index - pitch_lag_int*3 + (19 1/3)*3;
And for [85, 143] the pitch index is encoded as:
pitch_index = pitch_lag_int - 85 + (85 - 19 1/3)*3;
- pitch_lag_int
- integer pitch lag in the range [85, 143]
so...
else // only integer part encoded in range [85, 143], no fractional part pitch_lag_int = pitch_index - (85 - 19 1/3)*3 + 85; pitch_lag_frac = 0;
Second and fourth subframes
In the second and fourth subframes, the pitch lag resolution varies depending on the mode as follows:
- 7.95 kbps mode
- resolution of 1/3 is always used in the range [T1 - 10 2/3, T1 + 9 2/3]
- encoded using 6 bits => pitch_index is in the range [0, 63]
- 10.2 and 7.40 kbps modes
- resolution of 1/3 is always used in the range [T1 - 5 2/3, T1 + 4 2/3]
- encoded using 5 bits => pitch_index is in the range [0, 31]
- 6.70, 5.90, 5.15 and 4.75 kbps modes
- resolution of 1 is used in the range [T1 - 5, T1 + 4]
- resolution of 1/3 is always used in the range [T1 - 1 2/3, T1 + 2/3]
- encoded using 4 bits => pitch_index is in the range [0, 15]
Where T1 is nearest integer to the fractional pitch lag of the previous (1st or 3rd) subframe. The search range is bounded by [20, 143].
So the search range for the pitch lag is:
lower_bound = 5;
range = 9;
if(mode == 7.95) {
lower_bound = 10;
range = 19;
}
search_range_min = max(pitch_lag_int_prev - lower_bound, 20);
search_range_max = search_range_min + range;
if(search_range_max > 143) {
search_range_max = 143;
search_range_min = search_range_max - range;
}
- pitch_lag_int_prev
- the integer part of the pitch lag from the previous sub frame
For modes 7.40, 7.95 and 10.2 the pitch index is encoded as:
pitch_index = (pitch_lag_int - search_range_min)*3 + pitch_lag_frac + 2;
- pitch_lag_int
- the integer part of the pitch lag in the range [search_range_min, search_range_max]
- pitch_lag_frac
- the fractional part of the pitch lag in the range [-1, 1]
So the pitch lag is calculated through:
// integer part of pitch lag = position of pitch lag in range [search_range_min, search_range_max] + lower bound of the range pitch_lag_int = (pitch_index + 2)/3 - 1 + search_range_min; // fractional part of pitch lag = pitch index - (integer part without offset)*3 - 2/3 to bring the values to the correct range pitch_lag_frac = pitch_index - ((pitch_index + 2)/3 - 1)*3 - 2;
For modes 4.75, 5.15, 5.90 and 6.70:
t1_temp = max( min(pitch_lag_int_prev, search_range_min + 5), search_range_max - 4 );
- t1_temp
- predicted pitch lag from the previous frame adjusted to fit into the 0 position of the search range
The pitch index is encoded as:
// if pitch lag is below T1 - 1 2/3
if( pitch_lag_int*3 + pitch_lag_frac <= (t1_temp - 2)*3 ) {
// encode with resolution 1
index = (pitch_lag_int - t1_temp) + 5;
// else if pitch lag is below T1 + 1
}else if( pitch_lag_int*3 + pitch_lag_frac < (t1_temp + 1)*3 ) {
// encode with resolution 1/3
index = ( pitch_lag_int*3 + pitch_lag_frac - (t1_temp - 2)*3 ) + 3;
// else pitch lag is above T1 + 2/3
}else {
// encode with resolution 1
index = (pitch_lag_int - t1_temp) + 11;
}
- pitch_lag_int
- the integer part of the pitch lag in the range [search_range_min, search_range_max]
- pitch_lag_frac
- the fractional part of the pitch lag in the range [-1, 1]
The possible pitch indices and values are:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| -5 | -4 | -3 | -2 | -1 2/3 | -1 1/3 | -1 | -2/3 | -1/3 | 0 | 1/3 | 2/3 | 1 | 2 | 3 | 4 |
So the pitch lag is calculated through:
if(pitch_index < 4) {
// integer part of pitch lag = pitch lag position in range [t1_temp - 5, t1_temp - 2] + lower bound of range
pitch_lag_int = pitch_index + (t1_temp - 5);
// this range is coded with resolution 1 so no fractional part
pitch_lag_frac = 0;
}else if(pitch_index < 12) {
pitch_lag_int = (pitch_index - 2)/3 + (t1_temp - 2);
pitch_lag_frac = (pitch_index - 4) - ((pitch_index - 2)/3)*3 - 11;
}else {
// integer part of pitch lag = pitch lag position in range [t1_temp + 1, t1_temp + 4] + lower bound of range
pitch_lag_int = pitch_index - 12 + t1_temp + 1;
// this range is coded with resolution 1 so no fractional part
pitch_lag_frac = 0;
}
Calculate pitch vector
- k
- integer pitch lag
- n
- sample position in the vectors 0, ..., 39
- t
- 0, ..., 5 corresponding to fractions 0, 1/6, 2/6, 3/6, -2/6, -1/6 respectively
This equation can be used for both 1/3 and 1/6 resolution simply by multiplying t by 2 in the 1/3 case.
(Note: the coefficients b60 are in the reference source in an array called inter6)
Decoding of the fixed (innovative or algebraic) vector
- the excitation pulse positions and signs are parsed from the bit stream
- the pulse positions and signs are encoded differently depending on the mode
- the fixed code book vector, c(n), is then constructed from the pulse positions and signs
- if pitch_lag_int is less than the subframe size (40), the pitch sharpening procedure is applied
Decoding the pulse positions
12.2 kbps mode
- 10 pulse positions each coded using 3 bit Gray codes
- signs coded using 1 bit each for 5 pulse pairs
| Pulse | Positions |
|---|---|
| i0,i5 | 0, 5, 10, 15, 20, 25, 30, 35 |
| i1,i6 | 1, 6, 11, 16, 21, 26, 31, 36 |
| i2,i7 | 2, 7, 12, 17, 22, 27, 32, 37 |
| i3,i8 | 3, 8, 13, 18, 23, 28, 33, 38 |
| i4,i9 | 4, 9, 14, 19, 24, 29, 34, 39 |
10.2 kbps mode
- 8 pulse positions, 4 pairs, coded as 3 values using 10, 10 and 7 bits
- signs coded using 1 bit each for 4 pulse pairs
| Pulse | Positions |
|---|---|
| i0,i4 | 0, 4, 8, 12, 16, 20, 24, 28, 32, 36 |
| i1,i5 | 1, 5, 9, 13, 17, 21, 25, 29, 33, 37 |
| i2,i6 | 2, 6, 10, 14, 18, 22, 26, 30, 34, 38 |
| i3,i7 | 3, 7, 11, 15, 19, 23, 27, 31, 35, 39 |
7.95 and 7.40 kbps modes
- 4 pulse positions coded using 3, 3, 3 and 4 bits
- signs coded using 1 bit for each pulse
| Pulse | Positions |
|---|---|
| i0 | 0, 5, 10, 15, 20, 25, 30, 35 |
| i1 | 1, 6, 11, 16, 21, 26, 31, 36 |
| i2 | 2, 7, 12, 17, 22, 27, 32, 37 |
| i3 | 3, 8, 13, 18, 23, 28, 33, 38
4, 9, 14, 19, 24, 29, 34, 39 |
6.70 kbps mode
- 3 pulse positions coded using 3, 4 and 4 bits
- signs coded using 1 bit for each pulse
| Pulse | Positions |
|---|---|
| i0 | 0, 5, 10, 15, 20, 25, 30, 35 |
| i1 | 1, 6, 11, 16, 21, 26, 31, 36
3, 8, 13, 18, 23, 28, 33, 38 |
| i2 | 2, 7, 12, 17, 22, 27, 32, 37
4, 9, 14, 19, 24, 29, 34, 39 |
5.90 kbps mode
- 2 pulse positions coded using 4 and 5 bits
- signs coded using 1 bit for each pulse
| Pulse | Positions |
|---|---|
| i0 | 1, 6, 11, 16, 21, 26, 31, 36
3, 8, 13, 18, 23, 28, 33, 38 |
| i1 | 0, 5, 10, 15, 20, 25, 30, 35
1, 6, 11, 16, 21, 26, 31, 36 |
5.15 and 4.75 kbps modes
- 2 pulse positions coded using 1 bit for the position subset and 3 bits per pulse
- signs coded using 1 bit for each pulse
| Subframe | Subset | Pulse | Positions |
|---|---|---|---|
| 1 | 1 | i0 | 0, 5, 10, 15, 20, 25, 30, 35 |
| i1 | 2, 7, 12, 17, 22, 27, 32, 37 | ||
| 2 | i0 | 1, 6, 11, 16, 21, 26, 31, 36 | |
| i1 | 3, 8, 13, 18, 23, 28, 33, 38 | ||
| 2 | 1 | i0 | 0, 5, 10, 15, 20, 25, 30, 35 |
| i1 | 3, 8, 13, 18, 23, 28, 33, 38 | ||
| 2 | i0 | 2, 7, 12, 17, 22, 27, 32, 37 | |
| i1 | 4, 9, 14, 19, 24, 29, 34, 39 | ||
| 3 | 1 | i0 | 0, 5, 10, 15, 20, 25, 30, 35 |
| i1 | 2, 7, 12, 17, 22, 27, 32, 37 | ||
| 2 | i0 | 1, 6, 11, 16, 21, 26, 31, 36 | |
| i1 | 4, 9, 14, 19, 24, 29, 34, 39 | ||
| 4 | 1 | i0 | 0, 5, 10, 15, 20, 25, 30, 35 |
| i1 | 3, 8, 13, 18, 23, 28, 33, 38 | ||
| 2 | i0 | 1, 6, 11, 16, 21, 26, 31, 36 | |
| i1 | 4, 9, 14, 19, 24, 29, 34, 39 |
Fixed codebook vector construction
All c(n) are zero if there is no pulse at position n. If there is a pulse at position n then it has the corresponding sign as parsed above.
Pitch sharpening
- β
- the decoded pitch gain, ^g_p, bounded by [0.0,1.0] for 12.2. kbps or [0.0,0.8] for other modes
Decoding of the pitch and fixed codebook gains
Fixed gain prediction
A moving average prediction of the innovation (fixed) energy is conducted.
- g_c'
- fixed gain prediction
- \tilde{E}
- predicted energy [dB]
- \bar{E}
- desired mean innovation (fixed) energy [dB]
- E_I
- calculated mean innovation (fixed) energy [dB]
- b
- 4-tap MA prediction coefficients [0.68, 0.58, 0.34, 0.19]
- ^R(k)
- quantified prediction errors at subframe k (tabulated in ref source)
Desired mean innovation (fixed) energy:
| Mode (kbps) | Mean energy (dB) |
|---|---|
| 12.2 | 36 |
| 10.2 | 33 |
| 7.95 | 36 |
| 7.40 | 30 |
| 6.70 | 28.75 |
| 5.90 | 33 |
| 5.15 | 33 |
| 4.75 | 33 |
- E_I
- calculated mean innovation (fixed) energy [dB]
- N
- subframe size 40
- c(n)
- fixed codebook vector
Dequantisation of the gains
12.2kbps and 7.95kbps - scalar quantised gains
The received indices are used to find the quantified pitch gain, ^g_p, and the quantified fixed gain correction factor, ^γ_gc.
Pitch gain
The parsed gain index is used to obtain the quantified pitch gain, ^g_p, from the corresponding codebook. (qua_gain_pitch in the reference source.) In the 12.2 kbps mode, the two least significant bits are cleared.
Fixed gain correction factor
The parsed gain index is used to obtain the quantified fixed gain, ^g_c, from the corresponding codebook. (qua_gain_code in the reference source.) The table stores ^γ_gc, and the quantised energy error in two forms (these are needed for the moving average calculation of the predicted fixed gain):
qua_ener_MR122 = log2(^γ_gc) qua_ener = 20*log10(^γ_gc)
^γ_gc is stored at Q11 (i.e. it's multiplied by 2^11.) qua_ener_MR122 and qua_ener are stored at Q10.
Other modes - vector quantised gains
The received index gives both the quantified adaptive codebook gain, ^g_p, and the quantified algebraic codebook gain correction factor, ^γ_gc.
The tables contains the following data: ^g_p (Q14), ^γ_gc (Q12), (^g_c = g_c'*^γ_gc), qua_ener_MR122 (Q10), (log2(^γ_gc)) qua_ener (Q10) (20*log10(^γ_gc)) The log2() and log10() values are calculated on the fixed point value (g_fac Q12) and not on the original floating point value of g_fac to make the quantizer/MA predictdor use corresponding values.
Q: Should we bother using all the same tables at the same Q#? Should we calculate qua_ener* on-the-fly from ^γ_gc? A: log2 is fast on ints but generally log is quite slow. 20log10() standard expression for energy. If speed doesn't matter, calculate on the fly. My conclusion: Use tables, probably the ones from the reference source.
The codebook used depends on the mode:
6.70, 7.40, 10.2 kbps modes - table_gain_highrates in the reference source Four consecutive entries give ^g_p, ^γ_gc, qua_ener_MR122 and qua_ener. Apparently the values for qua_ener are the original ones from IS641 to ensure bit-exactness but are not exactly the rounded value of 20log10(^γ_gc).
5.15, 5.90 kbps modes - table_gain_lowrates Similar to table_gain_highrates, four consecutive entries give ^g_p, ^γ_gc, qua_ener_MR122 and qua_ener. There are no special notes for this table.
4.75 kbps mode - table_gain_MR475 Unlike the above mentioned tables, four consecutive values give ^g_p, ^γ_gc for subframes 0,2, and then ^g_p, ^γ_gc for subframes 1,3.
At the very least I think these tables could be redesigned a little.
Calculation of the quantified fixed gain
Smoothing of the fixed codebook gain
10.2, 6.70, 5.90, 5.15, 4.75 kbit/s modes only
Calculate averaged LSP vector
- \bar{q}(n)
- averaged LSP vector at frame n
- ^q_4(n)
- quantified LSP vector for the 4th subframe at frame n
Calculate fixed gain smoothing factor
- diff_m
- difference measure at subframe m
- j
- loops over LSPs
- m
- loops over subframes
- ^q_m
- quantified LSP vector at subframe m
- k_m
- fixed gain smoothing factor
- K_1
- 0.4
- K_2
- 0.25
- diff_m
- difference measure at subframe m
If diff_m has been greater than 0.65 for 10 subframes, k_m is set to 1.0 (i.e. no smoothing) for 40 subframes.
Calculate mean fixed gain
- \bar{g_c}(m)
- mean fixed gain at subframe m
- ^g_c(k)
- quantified fixed gain at subframe k
Calculate smoothed fixed gain
- ^g_c
- quantified fixed gain
- \bar{g_c}
- averaged fixed gain
Anti-sparseness processing
7.95, 6.70, 5.90, 5.15, 4.75 kbit/s modes only
Evaluate impulse response filter strength
The fixed vector, c(n), has only a few pulses per subframe. In certain conditions, to reduce perceptual artifacts arising from this, the vector is circularly convolved with a predefined impulse response. The selection of the strength of filter is made based on the decoded gains.
if ^g_p < 0.6 impNr = 0 else if ^g_p < 0.9 impNr = 1 else impNr = 2
- impNr = 0
- strong impulse response filter
- impNr = 1
- medium impulse response filter
- impNr = 2
- no filtering
if ^g_c(k) > 2 * ^g_c(k-1) impNr = min( impNr + 1, 2 ) else if impNr = 0 AND median of last five ^g_p >= 0.6 impNr = min( impNr(k), min(impNr(k-1) + 1, 2) )
Circular convolution of fixed vector and impulse response filter
- (c * h)
- convolution of vectors c and h, in this case circular convolution
- h[n]
- nth coefficient of the impulse response used for filtering
- c[n]
- nth coefficient of the fixed vector
n = 0, ..., 39
To make the convolution circular, make the impulse response circular by taking h[-m] = h[39-m]
Computing the reconstructed speech
Construct excitation
- u(n)
- excitation vector
- ^g_p
- quantified pitch gain
- v(n)
- pitch vector
- ^g_c
- quantified fixed gain
- c(n)
- fixed vector
Emphasise pitch vector contribution
This is apparently a post-processing technique.
- ^u(n)
- excitation vector with emphasised pitch vector contribution
- β
- ^g_p bounded by [0.0, 0.8] or [0.0, 1.0] depending on mode
Apply adaptive gain control (AGC) through gain scaling
- η
- gain scaling factor for emphasised excitation
- ^u'(n)
- gain-scaled emphasised excitation
Calculate reconstructed speech samples
- ^s(n)
- reconstructed speech samples
- ^a_i
- LP filter coefficients
Note: for n-i < 0, ^s(n-i) should be take from previous speech samples if existing, else we will consider them 0 as this behaviour is undefined the specification.
Additional instability protection
If an overflow occurs during synthesis, the pitch vector, v(n), is scaled down by a factor of 4 and synthesis is conducted again bypassing emphasising the pitch vector contribution and adaptive gain control.
Q: What classifies an overflow? A: s(n) < -32768 or s(n) > 32767 (i.e. 16-bit signed int)
Post-processing
Adaptive post-filtering
(c.f. §6.2.1)
IIR filtering
The speech samples, ^s(n), are filtered through a formant filter and a tilt compensation filter.
- γ_n, γ_d
- control the amount of formant post-filtering
The speech samples, ^s(n), are filtered through ^A(z/γ_n) to produce the residual signal ^r(n).
^r(n) is filtered through 1/^A(z/γ_d).
The output is filtered through H_t(z) (the tilt compensation filter) resulting in the post-filtered speech signal, ^s_f(n).
- L_h
- 22 - the truncation of the impulse response
- h_f
- impulse response of the formant filter H_f
So, in summation notation:
12.2 and 10.2 kbps modes
γ_n = 0.7
γ_d = 0.75
γ_t = 0.8 if k_1' > 0; 0 otherwise
Other modes
γ_n = 0.55
γ_d = 0.7
γ_t = 0.8
Adaptive gain control
Adaptive gain control is used to compensate for the gain difference between the filtered and synthesised speech signals.
- \alpha
- adaptive gain control factor equal to 0.9
High-pass filtering and upscaling
(c.f. §6.2.2)
After completing all filtering, the samples are scaled up by a factor of 2.